Roulette Probability Formula
Understanding the Probability
In 2012, a group of physicists from Hong Kong Polytechnic University visited casinos with a laser measuring instrument and a range of equipment. This was a scientific experiment made with permission from the authorities. They were testing the “chaos theory” and wanted to see if they can predict where the ball will land beforehand on a roulette wheel. They calculated the speed of the wheel and the ball even measured the air resistance. The results were surprising: Despite all these scientific equipment, the success rate was only 59%. They were able to make 18% profit in the long run. This was quite an impressive achievement, as this ratio is -2.7% for ordinary players. But at the same time, it showed that probability calculations were only up to 60% accurate even when scientific instruments were used. (You can visit Slotozilla to read other articles about possibility calculations in casino games.)
Using the probability mass function and summation notation allows us to more compactly write this formula as follows, where the summation is taken over the index i: E( X ) = Σ x i f ( x i ). This version of the formula is helpful to see because it also works when we have an infinite sample space. Probabilities for Roulette. Since the spaces are the same size, the ball is equally likely to land in any of the spaces. This means that a roulette wheel involves a uniform probability distribution. The probabilities that we will need to calculate our expected value are as follows.
We do not have such devices, so we have to resort to “classical” methods. In this article, we will talk about both probability calculations and easy & new methods of calculating possibilities. Let us first explain what probability implies: Simply put, it means calculating the probability of an outcome. To simplify even more, let us consider two digits: 0 and 1. Imagine a long line, 0 on one end and 1 on the other end. If the probability of a result is too small, it will be placed near 0, and we will place it near 1 if it is a high possibility.
Now imagine a European roulette wheel: There are exactly 37 numbers on it. How do you calculate the probability of an exact number? Mathematically it is quite easy to do: You divide 1 into 37. The result is 0.27. Now let’s go back to the line above: If you play a roulette and wager on a certain number, the probability of this happening will be very close to 0, right? In other words, your chances will be very, very low.
Roulette Probabilities
You can use this formula for all types of betting. In this way, it is also possible to understand what your chances are for each bet. Considering this, the betting options with the highest probability in roulette are 3 in total. Let’s do the calculation together:
Roulette Probability Chart
- There are 18 single, 18 double numbers on the roulette wheel
- Roulette wheel has 18 black, 18 red colors
- Of the total 36 numbers, 18 are above the table, and 18 are below.
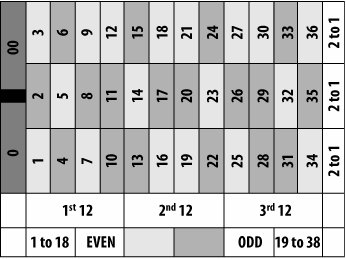

The first option corresponds to the odd / even bet. The second is known as red/black and the third as column/row bet. Regardless of the scope, you are betting on a total of 18 numbers. Let’s apply the formula above: 18/37 = 48.65%. In other words, you have a very good chance of winning with these types of bets. You can also verify this with a Venn diagram, but there is no need to complicate it. For all the betting options, you can easily see what your chances of winning by dividing the total number into 37. You can even use this formula for many other table games. Let’s give an example from the Craps game: When you throw the dice, what is the probability of landing a “5”? You are betting on one option, and the dice have 6 faces, i.e., 1/6 = 16.67%. This simple formula is also important in terms of learning the most basic roulette strategies. Even if you do not know a specific tactic, you can do simple probability calculations in all games with this process.
Roulette “Systems”
For the same reason, you can understand why roulette “systems” are useless. Martingale and similar systems are based on the assumption that the probability calculations will ultimately yield a positive result. For example, if the result is black 10 times, the eleventh result should be red – black is too “hot” right now. Or they just bet on a certain number, and they believe it will eventually come out. This is called the “gambler’s fallacy”. Theoretically, this is true: If you wait long enough, you will ultimately win the number or option you bet on. However, the numbers on the roulette wheel can be arranged 14,355,594,379 times differently. So you may have to wait for a longer period than you anticipate! All roulette probabilities are calculated from scratch every time. Remember the 48.65% rate we gave you above? That rate is always the same, and even if you play for the thousandth time, it never changes. For this reason, none of the roulette systems will work. The only thing you can do is to place your bets into most likely odds and hope to be lucky enough.
:max_bytes(150000):strip_icc()/expected-5733972a5f9b58723d773687.png)

/close-up-of-roulette-wheel-1059428626-0bfd3dca97294b6f915f791deece0ef4.jpg)
Roulette Probability Formula Calculator
- Unfortunately, it is mathematically impossible for any of these systems to work. Many people still don’t understand the basic probability of roulette, and the fact that each new spin of the wheel has independent odds. A casino has an edge over anyone who plays roulette (generally 5.26% on an American style table).
- Here is how you should do the roulette probability formula: P(Red) x A (value for red) + P(Not red) x A (value that is not red) = 18/37 + 2 + 20/37x (-1) = 0.4865. Interpreting the results of the probability roulette calculator.